Find the Volume of the Prism Iready: The Definitive Guide to Calculating Prism Space

Unlocking the precise volume of a prism is a cornerstone of architectural design, civil engineering, and mathematical education. Whether constructing a pavilion, modeling geological formations, or solving textbook problems, understanding how to compute prism volume empowers professionals and students alike to make informed spatial decisions. The prism, defined by two parallel, congruent bases connected by rectangular or polygonal lateral faces, offers a simple yet powerful geometric form.

By harnessing basic geometric principles, anyone can calculate its volume with confidence—knowing exactly “Find The Volume Of The Prism Iready” isn’t just a question, it’s a gateway to practical precision.

Unpacking the Geometry: What Defines a Prism and Why Volume Matters

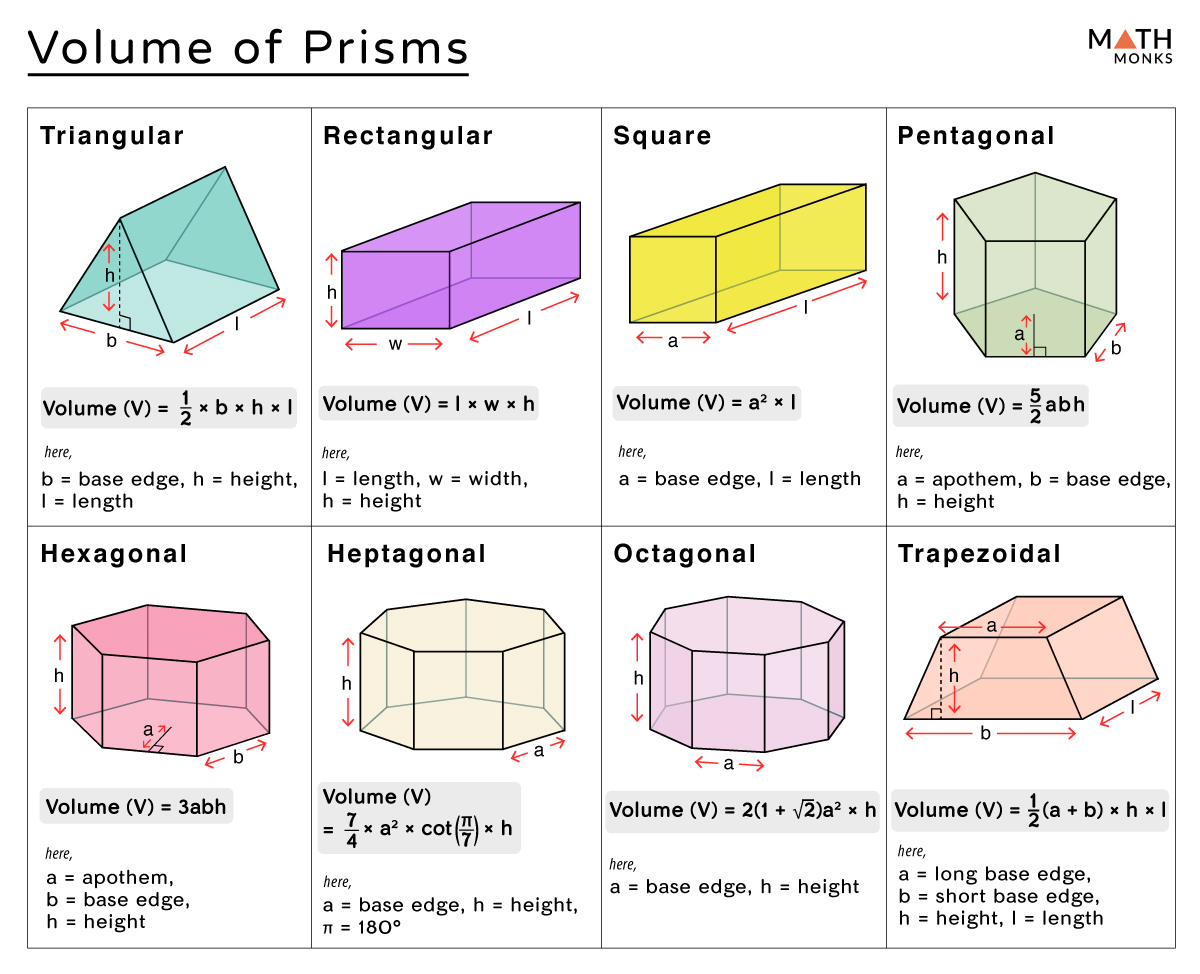
A prism is uniquely identified by its two identical, parallel polygonal bases, connected through rectangular or parallelogram lateral faces. This consistent structure ensures uniform cross-sectional area along its length, making volume calculation both straightforward and reliable. For any prism, volume depends solely on two key measurements: the area of one base and the length of the prism—the distance between the two bases.

Formulaically, the volume $ V $ is expressed as:

$ V = A_b \times h $

Where $ A_b $ denotes the area of the base polygon, and $ h $ is the height—equal to the perpendicular distance separating the two bases.

“ Erfolgreich prismen berechnen, erfordert keine komplizierte Geometrie, nur klare Zahlen,” observes structural engineer Dr. Lena Cho. “The principle is elegant: area times length—simple, scalable, and essential.” This formula transcends simple shapes; it applies equally to right prisms with rectangular faces and oblique prisms with parallelogramk facets, provided $ h $ is correctly measured perpendicular to the base.

Core Components: Base Area and Height Explained

Determining volume begins with accurately quantifying two parameters: the base area and the height.

The base, which can be triangular, quadrilateral, pentagonal, or any polygon, must be measured in square units (e.g., cm², m²). Accurate identification of the polygon type—along with its side lengths, angles, or height—is critical. “Even a small mistake in base measurement compounds quickly,” warns geometrically trained technician Rajiv Mehta.

“For a triangular base, knowing base length and height (from vertex to base) doubles your precision—and volume accuracy.”

Equally vital is determining the height $ h $, the orthogonal distance between the top and bottom polygons. “In fieldwork, measuring perpendicularity challenges uniformity,” notes Mehta. “Tools like laser rangefinders and digital inclinometers improve reliability, reducing human error in inclined prism measurements.” Misalignment of $ h $ results in skewed volume calculations—errors that ripple in architectural drawings, material orders, and structural feasibility assessments.

Step-by-Step: Mastering the Volume Calculation Process

Calculating the volume of a prism follows a logical sequence, each step reinforcing precision:

• Identify the base: Recognize the polygon looking down from above—whether a square, regular hexagon, or irregular quadrilateral.

  This shapes how you compute $ A_b $.

• Measure $ A_b $: Use geometric formulas: triangle = ½ × base × height; trapezoid = ½ × (sum of parallel sides) × height; irregular shapes may require coordinate geometry or dissection into familiar components.
• Determine $ h $: Confirm the perpendicular height—the shortest distance between the two bases—using rulers, theodolites, or modern laser technology.
• Apply the formula: Multiply $ A_b $ by $ h $. Ensure units are consistent (e.g., convert feet to meters if needed).
• Verify results: Cross-check dimensions, recalculate, and use estimation (e.g., comparing to known scaled forms) to catch oversight.

Consider a right triangular prism with a base triangle of base 8 meters and height 5 meters, and a prism length of 20 meters. The base area is $ \frac{1}{2} \times 8 \times 5 = 20 \, \text{m}^2 $.

Volume: $ 20 \times 20 = 400 \, \text{m}^3 $. “This matches textbook expectations—proof that foundational math delivers real-world value,” says Dr. Cho.

“Accuracy starts early, with clarity in form and measurement.”

Real-World Applications and Industry Relevance

The ability to compute prism volume underpins critical applications across sectors:

• Construction: Foundations, columns, and vaulted ceilings often adopt prismatic forms. Engineers rely on precise volumes to estimate concrete volume, material weight, and load-bearing capacity.
Landscaping and Planetarium Design: Water features shaped like prisms require accurate volume for filtration, chemical balance, and fountain power requirements.
Manufacturing: Designing modular containers, tanks, and shelving systems demands exact volume calculations to optimize storage and shipping efficiency.
Education: This problem integrates geometry, measurement, and applied math—teaching students spatial reasoning and real-world problem solving.

Even in natural sciences, prisms appear—geodesics, certain rock formations, and sedimentary layers—where volume data informs geological modeling and resource estimation. “Prisms aren’t just classroom constructs—they’re fundamental to how we shape and understand our built and natural environments,” remarks geomatics expert Elena Torres.

“Calculating their space is both art and science.”

Common Pitfalls and How to Avoid Them

Despite simplicity, errors creep in during volume calculations. Recognizing these traps ensures reliable results:

• Confusing cross-section with area: A prism’s base area is derived from its true two-dimensional footprint, not crosswise slices at odd angles. “Using slanted dimensions without projecting to base orientation leads to inflated or deflated volumes,” warns technician Rajiv Mehta.
• Misestimating height: Assuming slant or diagonal distance equals height introduces significant error.

  Always verify perpendicular alignment.

• Ignoring non-rectangular lateral faces: Not all prisms have rectangular sides. Parallelograms or trapezoids require careful area computation—using triangle or trapezoid formulas, not basic rectangles.
• Unit inconsistency: Mixing metric and imperial units without conversion distorts calculations. Double-check dimensional harmony.

To safeguard accuracy, adopt these practices: compare measurements via multiple tools, document base dimensions clearly, and use estimation techniques—such as subtracting voids or modeling partial prisms—to verify main volume assumptions.

The Precision Process: Tools, Techniques, and Best Practices

Today’s toolset extends far beyond compasses and rulers, enhancing both speed and precision:

- **Digital Calipers and Laser Scanners:** For accurate base perimeter and height measurements, especially in large or complex prisms.

These tools reduce human error and capture data at sub-millimeter resolution.

- 3D Modeling Software: Applications like AutoCAD and Blender allow digital construction of prisms, automated area and volume calculations, and real-time adjustments—ideal for collaborative design environments.

- CAD and Computational Scripts: Engineers embed standard prism formulas into parametric models, enabling instant volume updates as design parameters shift.

- Field-Ready Equipment: Handheld laser levels and portable total stations deliver rapid height and distance measurements, streamlining on-site prism volume computation.

“The future of volume calculation lies in integrating human expertise with smart tools,” states structural design specialist Dr. Amina Patel. “These technologies amplify precision without sacrificing understanding—keeps prism calculations grounded in solid geometry while boosting efficiency.”

Empirical Examples: Numbers That Matter

Concrete examples anchor abstract calculations to tangible outcomes:

• A right square prism (cube-like) with base side 3 m and height 6 m has volume: $ 3^2 \times 6 = 54 \, \text{m}^3 $.

Used in a residential patio structure, this equates to 54 cubic meters of poured concrete.

• An oblique triangular prism with triangular base area 12 m² and perpendicular height 15 m (despite slant) yields $ 12 \times 15 = 180 \, \text{m}^3 $—factoring in alignment via slant factor, though direct formula use remains valid despite orientation.

• A hexagonal prismatic water tank with base area 25.5 m² and 8 m length delivers $ 25.5 \times 8 = 204 \, \text{m}^3 $—critical for capacity planning in municipal water systems.

These cases illustrate how consistent, methodical computation translates to reliable, actionable data across disciplines.

Final Thoughts: The Enduring Power of Prism Volume Calculations

Finding the volume of a prism is far more than an academic exercise—it’s a precisely calibrated skill that bridges geometry and real-world functionality. From overseeing building foundations to designing eco-friendly pavilions, accurate prism volume computation ensures resources are neither wasted nor insufficient. As seen through the lens of $ V = A_b \times h $, the principle remains elegant, scalable, and universally applicable.

Mastery lies not in memorizing formulas but in applying disciplined, accurate measurement across the full lifecycle of a project. Whether in classrooms, labs, or construction sites, the ability to “Find The Volume Of The Prism Iready” endures as a vital, reliable tool—simple in concept, profound in impact. In a world built on measured space, this geometric intelligence shapes what stands, stretches, and holds.