How To Change Standard Form to Vertex: The Precision Formula Every Student and Professional Needs

From equations on a whiteboard to real-world modeling, translating standard form into vertex form unlocks deeper mathematical insight—especially in quadratic equations. Standard form, typically written as \( ax^2 + bx + c \), lay a foundation, but vertex form \( a(x - h)^2 + k \) reveals the precise center point—the vertex—where parabolas peak or dip. Mastering this transformation isn’t just academic—it’s essential for solving optimization problems, graphing with accuracy, and interpreting physics and economics models.

This guide cuts through complexity to deliver a clear, step-by-step method, supported by examples and practical context.

The Hidden Power of Vertex Form in Mathematics

While standard form is intuitive for finding roots and graph intercepts, vertex form reveals a parabola’s visual and analytical core. The vertex—coordinates \((h, k)\)—tells the exact location of the minimum or maximum value, critical in applications like projectile motion, revenue maximization, and cost minimization.

“Vertex form transforms abstract coefficients into physical meaning,” notes Dr. Elena Torres, higher education math specialist. “It turns abstract numbers into locators—pointing exactly where a parabola turns, whether rising or falling.” This shift enables engineers, data scientists, and educators to analyze and predict behavior with surgical precision.

Why Standard Form Falls Short—And How Vertex Form Fixes It

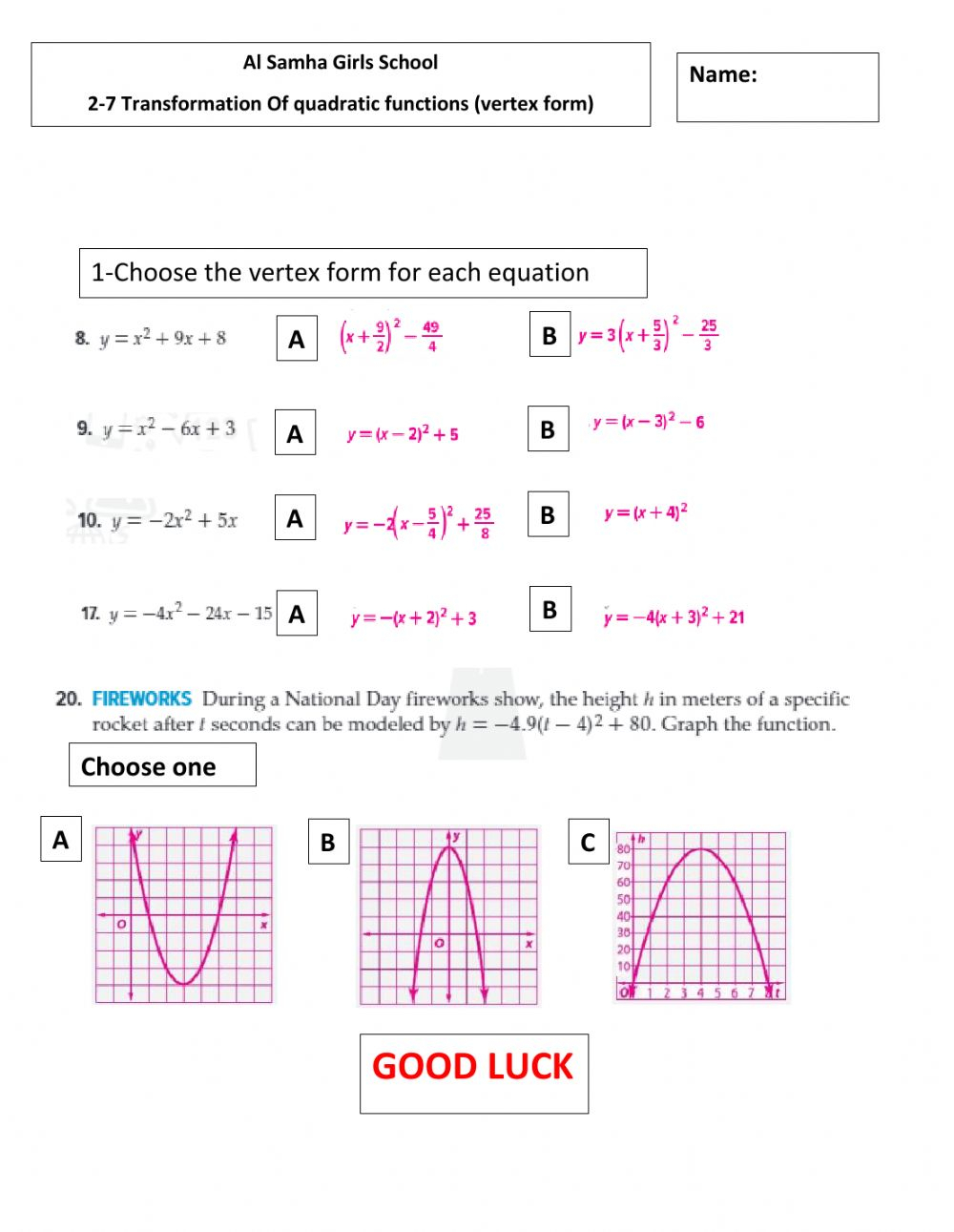
Standard form \( ax^2 + bx + c \) captures the full quadratic expression but obscures the precise center. To find key features like vertex or axis of symmetry, one must perform additional calculations. Transitioning to vertex form unlocks these insights instantly.

```math a(x - h)^2 + k ``` Here, \( h = -\frac{b}{2a} \) and \( k = f(h) \)—a formula derived from completing the square. This transformation is not merely algebraic manipulation; it’s a reframing of the equation’s geometry, placing the parabola’s peak or trough at the vertex. Without this step, complex real-world modeling becomes a guessing game rather than a data-driven discipline.

The Step-by-Step Transformation: From ax² + bx + c to a(x - h)² + k

Converting standard form to vertex form relies on completing the square—a method as foundational as it is powerful. The core steps unfold with mathematical elegance: 1. **Verify Standard Form**: Ensure the equation is in the form \( ax^2 + bx + c \), with \( a \ne 0 \).

2. **Factor Out the Coefficient \( a \)**: Extract \( a \) from the quadratic and linear terms to simplify exponent handling. 3.

**Complete the Square**: Use the expression inside the parentheses to form a perfect square trinomial. 4. **Complete the Square Mathematically** - Take half of the coefficient of \( x \), square it, and add and subtract it within the parentheses.

- Example: For \( ax^2 + bx \), rewrite as \( a\left(x^2 + \frac{b}{a}x\right) \), then add and subtract \(\left(\frac{b}{2a}\right)^2\). 5. **Rewrite in Vertex Form**: Group the squared term and complete the constant shift to match \( a(x - h)^2 + k \).

6. **Identify Vertex Coordinates**: The value \( h \) appears as \( -\frac{b}{2a} \); substitute into the equation to find \( k = f(h) \). Each phase advances understanding: from isolating \( a \) to reshaping expressions, every refinement sharpens both computation and conceptual clarity.

Step-by-Step Demonstration: Turning x² – 6x + 5 into Vertex Form

Consider the quadratic \( f(x) = x^2 - 6x + 5 \). Applying the full transformation: - **Step 1**: Confirm \( a = 1 \), fully in standard form. - **Step 2**: Coefficient of \( x \) is \(-6\), so factor: \( 1(x^2 - 6x) + 5 \).

- **Step 3**: Complete the square: - Half of \(-6\) is \(-3\), squared is \(9\). - Add and subtract \(9\): \( 1(x^2 - 6x + 9 - 9) + 5 \). - **Step 4**: Rewrite: \( f(x) = 1[(x - 3)^2 - 9] + 5 = (x - 3)^2 - 9 + 5 = (x - 3)^2 - 4 \).

- **Step 5**: Extract vertex form: \( f(x) =