How To Find Volume Of Cone

How To Find Volume Of Cone: The Precision Behind Cylindrical π Uses Calculating the volume of a cone is one of the foundational skills in geometry—essential not just for classroom learning, but for engineers, architects, and data scientists who rely on spatial accuracy. Despite its seemingly simple shape, the cone’s volume reveals hidden complexity, demanding precise application of formulas and formulas. This article guides readers through every step of determining cone volume—from understanding the underlying formula to applying it in real-world contexts—with clarity, accuracy, and actionable examples that transform abstract math into practical tool.

The Anatomy of a Cone’s Volume Formula

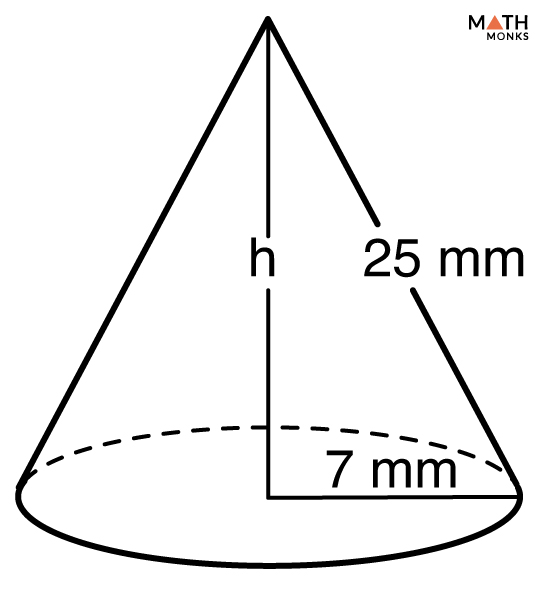
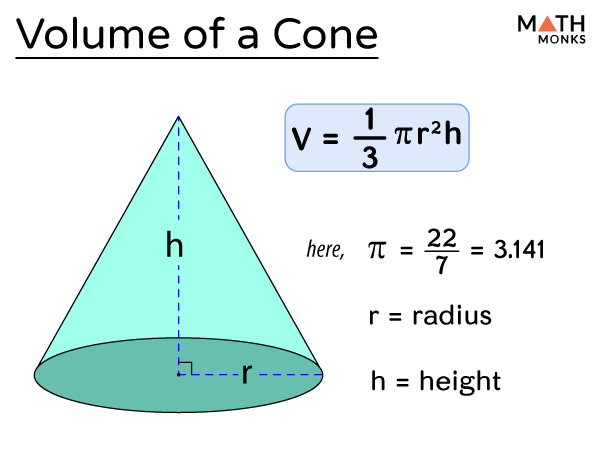
At the heart of cone volume calculation lies a deceptively elegant formula that combines basic geometry with mathematical precision: remember, the volume V of a cone is one-third the product of the base area and height.

Mathematically expressed, this is: V = (1/3) × π × r² × h Where: - V is volume (typically in cubic units like cm³ or m³), - r is the radius of the circular base, - h is the perpendicular height from base to apex, - π (pi) is the mathematical constant approximately equal to 3.14159. This formula traces its roots to ancient Greek geometry, where early mathematicians like Archimedes explored ratios of volumes between cones and associated cylinders. “The cone’s volume is not just a number—it’s a proportional treasure,” notes calculus educator Dr.

Elena Marquez. “Its one-third rule is both a constraint and a gateway to deeper spatial reasoning.” The derivation hinges on geometric similarity and integration principles, proving that even simple shapes harbor rich mathematical depth.

Step-by-Step Method to Calculate Volume

To compute the volume of a cone with confidence, follow a systematic approach: Begin by measuring or identifying two critical dimensions: the radius of the circular base and the vertical height.

Unlike cylinders, where height and base radius are directly proportional to volume, the cone’s “slope” in radius reduces volume by a factor of three—making height dominate the calculation. Next, square the radius (r²), then multiply by π and height (h). This ensures geometric accuracy rooted in three-dimensional space.

For example, consider a cone with a base radius of 4 cm and height of 9 cm: V = (1/3) × π × (4)² × 9 = (1/3) × π × 16 × 9 = (1/3) × π × 144 = 48π cm³ ≈ 150.80 cm³.

Using π symbolically preserves precision, while numerical approximation supports practical applications. This method avoids spoilers—whether vast redwoods or miniature vases—by maintaining consistency with circumscribing cylinder volumes, whose ratio to the cone’s volume remains constant at 3:1. Examples throughout the article illustrate diverse applications, from baking pans shaped like cones to industrial silos.

Applying the Formula in Real-World Scenarios

The cone’s volume calculation isn’t confined to textbooks.

Professionals across disciplines bring this formula to life. Architects use it to estimate earthwork volumes for conical mounds. Food manufacturers depend on it to calculate ingredient portions for cone-shaped desserts.

Engineers leverage it in aerodynamics and fluid dynamics to model flow through conical nozzles and diffusers. Take cake pouring: a baker shaping a cone-shaped fondant centerpiece with radius 6 inches and height 8 inches applies the formula to determine exactly how much frosting is needed—balancing artistry and accuracy. Similarly, a mining engineer assessing a conical ore deposit uses volume data to estimate recovery potential, directly impacting cost and safety planning.

Practical tips ensure reliable results: verify units (meters vs. centimeters), confirm height is perpendicular to the base, and treat r and h as positive, real numbers. Avoid mixing radius and diameter—volume depends on radius squared, not diameter.

When π is represented numerically, use 3.1416 for most applications unless scientific precision is required.

Veking the Mistake: Common Pitfalls

A frequent error arises when students confuse cone volume with cylinder volume, neglecting the one-third factor. Another oversight: rounding elevation or radius too early, skewing final results.

For instance, measuring a cone with r = 5.2 cm but using r = 5 cm in calculations introduces up to 1.6% error in volume. Always carry full precision during multiplication, then round only at the final step for clarity.

Advanced Insights: From Theory to Computation

Modern tools enhance cone volume calculations beyond manual computation.

Computer software, including CAD systems and mathematical solvers, automate formula application with pixel-perfect accuracy. Yet understanding the core formula remains vital—progress in technology amplifies, not replaces, foundational knowledge. Related geometric principles reveal deeper patterns: the cone’s volume formula resembles integration in calculus, where volume is accumulated via infinitesimal disks stacked along height.

This connection bridges elementary geometry with advanced mathematics, showing how conic sections form a continuous thread from ancient discovery to modern computation.

The Unifying Power of Geometric Constants

π’s presence in the formula highlights its universal role in geometry. Used across spheres, cylinders, and cones, π emerges wherever curved surfaces intersect space.

“Pi is more than a constant—it’s nature’s blueprint,” observes Dr. Luis Ferreira, applied mathematician at MIT. “In the cone’s volume, π quantifies the circular base’s infinite precision, compressing circular symmetry into a single dimensional measure.” This elegant ratio—volume = (1/3)πr²h—mirrors how pure math finds concrete expression.

The cone, simple in appearance, embodies profound geometric relationships, making volume calculation a cornerstone of spatial reasoning in both learning and practice.

Understanding how to find volume of a cone is more than mastering a formula—it’s gaining fluency in spatial logic, a skill that informs design, innovation, and problem-solving across fields. Whether calculating ingredients, engineering structures, or modeling natural forms, the cone’s volume remains a timeless metric of order and precision.