LCM 18 and 12: The Mathematical Bridge That Unlocks Classroom Logic and Real-World Precision

In the intricate tapestry of number theory, few combinations reveal as much about structure and function as the least common multiple (LCM) of 12 and 18. Though deceptively simple, the LCM of these two integers—12 and 18—serves as a foundational concept in mathematics education, computer science, scheduling, and periodic events, illuminating how numbers align through shared rhythm and frequency. Understanding LCM 18 and 12 unveils not just a numeric result, but a powerful tool for solving practical problems across disciplines.

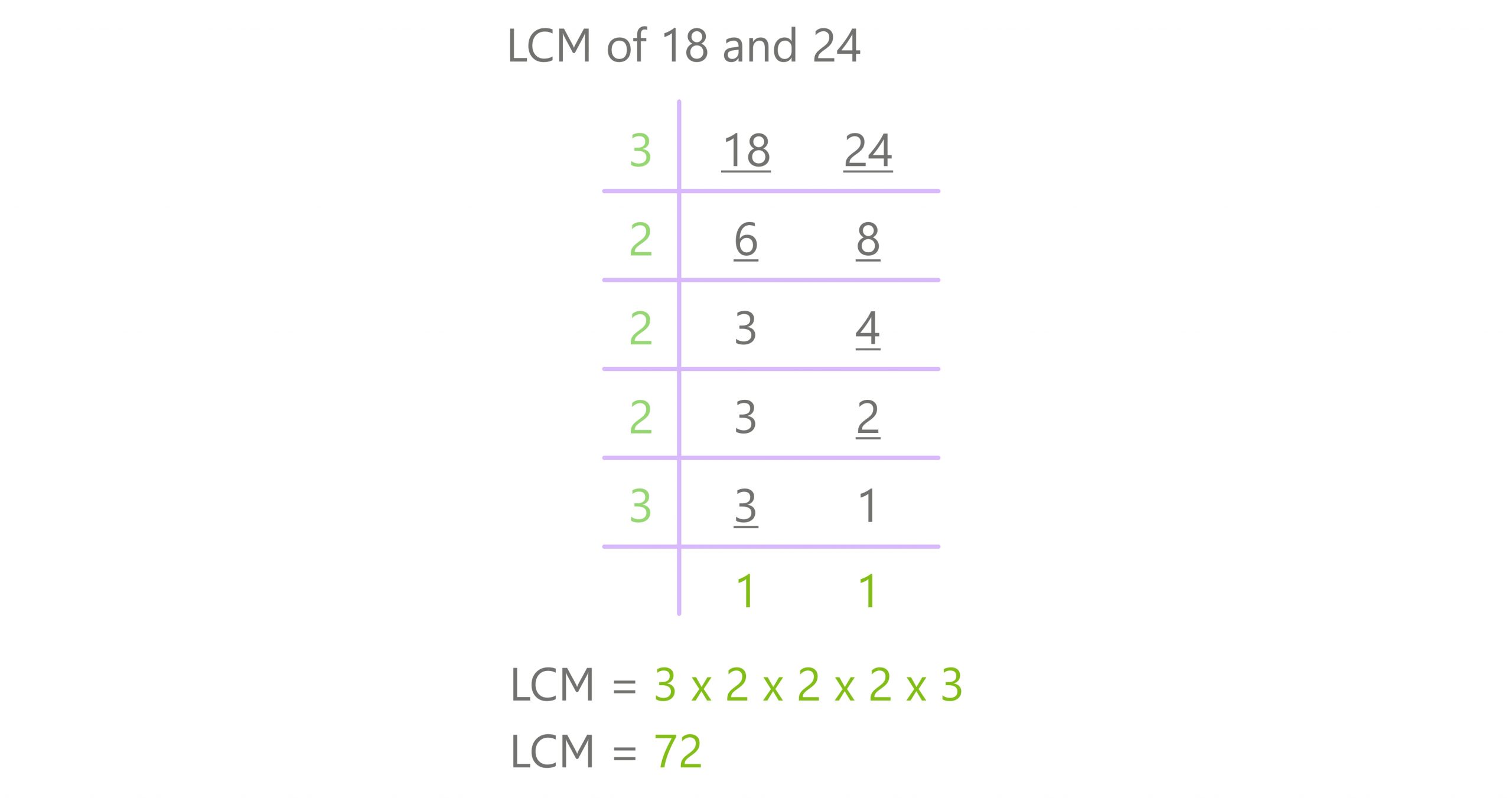
At its core, the least common multiple of two or more integers is the smallest positive number divisible by each of them without remainder. For 12 and 18, this value is not arbitrary—it emerges from a precise mathematical relationship rooted in prime factorization. Breaking down the numbers, 12 factors into 2² × 3, while 18 decomposes into 2 × 3².

The LCM is determined by taking the highest power of each prime: 2² from 12 and 3² from 18, yielding 4 × 9 = 36. Thus, LCM(12, 18) = 36.

This result carries immediate symbolic weight.

The number 36 marks a natural convergence point for multiples of both 12 and 18, enabling efficient coordination of recurring cycles:

• ​Timekeeping & Scheduling: If one bus route cycles every 12 minutes and another every 18 minutes, they synchronize every 36 minutes, optimizing passenger transfers.
• ​Geometry & LCM Applications: In tiling or pattern design, x-year cycles aligning every 36 units allow seamless integration of repeated motifs.
• ​Data Processing & Algorithms: In computing, LCM aids buffer sizing—oputations demanding synchronized data streams every 36 bytes rely on this multiple for efficiency.

Beyond pure math, LCM 18 and 12 exemplifies how abstract theory fuels real-world logic. In education, teaching the LCM builds fluency in divisibility, primes, and multiples—building blocks for algebra, cryptography, and engineering. For example, when planning multi-day school events requiring synchronized routines (science fairs, assemblies, or sports), aligning schedules at 36-minute intervals ensures smooth transitions and minimizes conflicts.

As Dr. Elena Torres, applied mathematician at the Institute for Quantitative Learning, notes: “LCM is the silent architect of harmony in recurring systems—it’s how we make chaos predictable.”

In number theory, the LCM reveals deeper insights: - Both 12 and 18 are divisors of 36, confirming it as their least shared multiple. - 36 is also the smallest number for which 12 and 18 share a common period—critical in modular arithmetic and cyclic function design.

- The greatest common divisor (GCD) of 12 and 18 is 6, and the identity LCM(a,b) × GCD(a,b) = a × b confirms this: 12 × 18 = 216; 6 × 36 = 216.

Historically, divisibility and multiples have guided human organization long before formal math. Ancient calendars, though less precise, intuitively followed similar cycles—annual harvests, lunar phases, and religious festivals repeating in interwoven rhythms. The LCM of core numbers like 12 (months, hours) and 18 (seasonal markers in some cultures) echoes this ancestral synchronization.

In architecture and design, repeating patterns based on LCM multiples ensure visual coherence—think tiled mosaics where 12-unit and 18-unit tiles align perfectly every 36 units without mismatch.

Computationally, LCM 18 and 12 underpins efficient operations. In programming, calculating LCM enables optimized task scheduling—processes running every 12 and 18 cycles can run in lockstep at 36-cycle intervals, reducing overhead and latency.

Network protocols, data encryption, and even digital signal processing exploit this principle: by leveraging multiples, systems maintain symmetry and reduce computational complexity.

Using visual aids strengthens comprehension:

1. Prime factor decompositions: 12 = 2²×3, 18 = 2×3² → LCM = 2²×3² = 36
2. Multiples list: Multiples of 12: 12, 24, 36, 48… Multiples of 18: 18, 36, 54… First shared multiple: 36
3. Graphical representation: A number line marked every 6 units highlights how 36 is the first point where multiples overlap.

The synergy of 12 and 18 in their LCM transcends arithmetic—it embodies order emerging from intersection. Where two numbers appear independent, their 36th multiple reveals a design philosophy: efficiency through alignment, harmony through repetition, precision through shared frequency.

In classrooms, engineers, scientists, and programmers alike rely on this convergence, turning abstract concepts into tools that shape how systems function.

Far more than a classroom exercise, the LCM of 18 and 12 exemplifies how foundational mathematics fuels innovation. Whether coordinating city transit, designing resilient software, or planning school schedules, the principle of LCM remains indispensable.

It is not merely a number—it is a bridge between numbers and function, a testament to the elegance embedded in simple arithmetic.