The Steady Pulse of Trigonometry: How Sine, Cosine, and Tangent Power Technology, Navigation, and Engineering

From ancient star charts in Babylon to the precise flight algorithms guiding commercial jets, the trigonometric functions sine, cosine, and tangent remain foundational to how we measure angles, distances, and motion. These three ratios—derived from right triangles and extended through the unit circle—are far more than abstract math concepts; they form the backbone of modern science, enabling accurate calculations that shape everything from smartphone navigation to satellite orbits. By unraveling the roles of sine, cosine, and tangent, we uncover a silent but essential language embedded in technology, construction, and exploration.

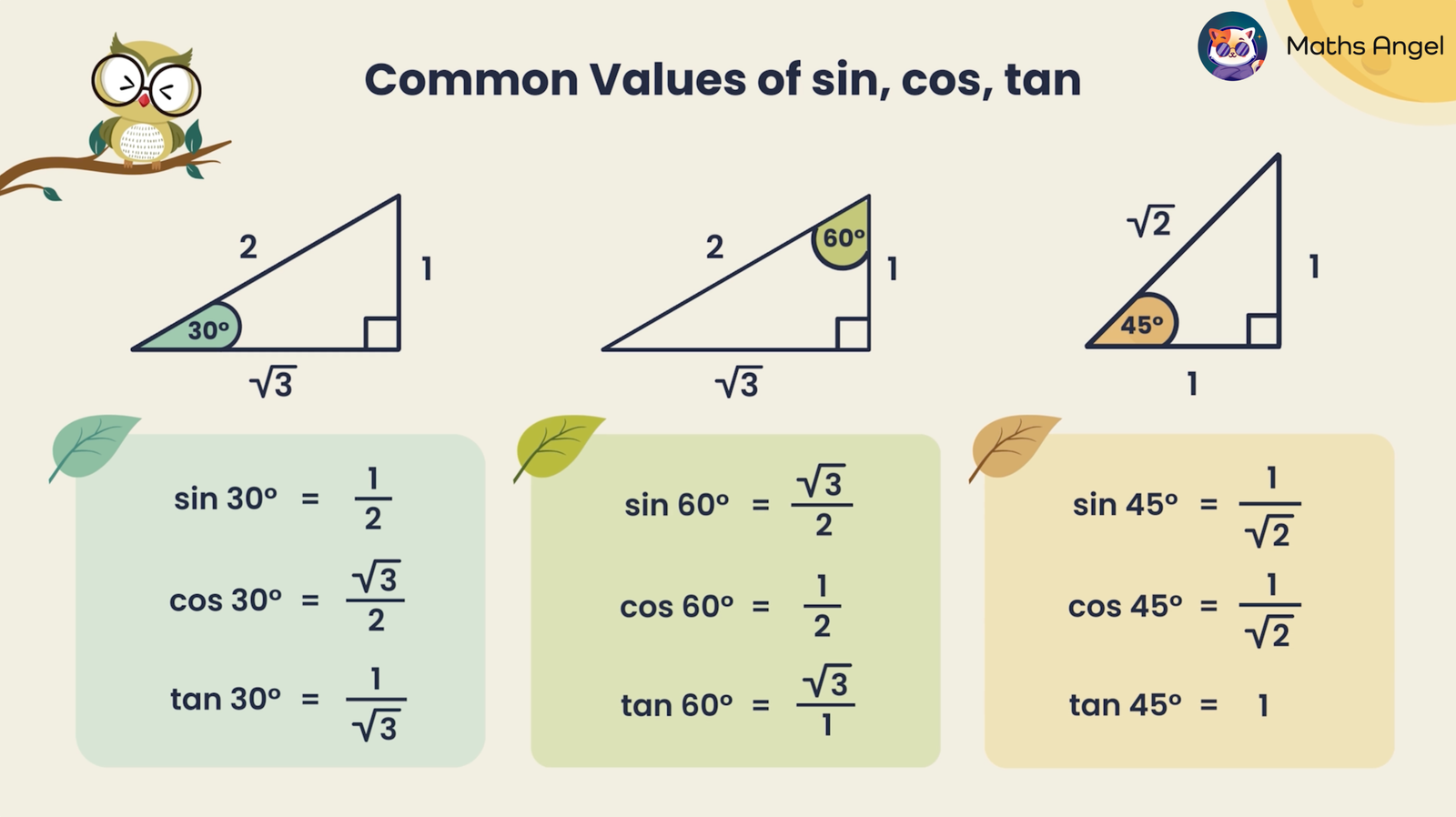
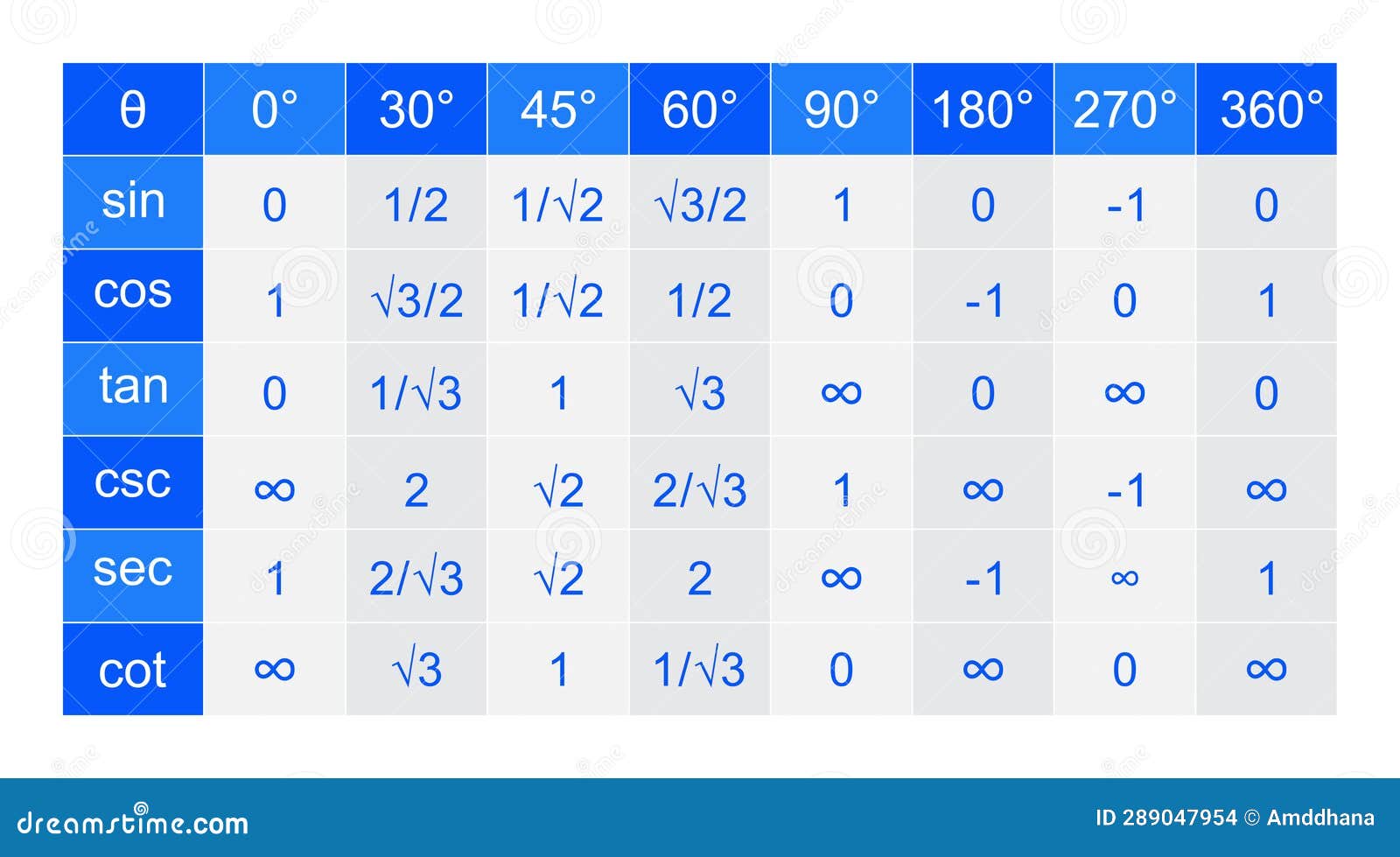
At their core, sine, cosine, and tangent connect length to angle in right triangles: sine compares the opposite side over the hypotenuse, cosine relates adjacent over hypotenuse, and tangent links opposite to adjacent.

But their true power lies in extension—through the unit circle, applying to all angles and even negative values, and via complex numbers, where they bridge algebra and geometry. This versatility has transformed theoretical math into practical tool, forming the backbone of coordinate systems and signal processing.

Historical Roots: From Astronomy to Architecture

Ancient civilizations relied on early trigonometric principles long before formal notation. Babylonian astronomers tracked celestial movements using angular measurements, while Greek mathematicians like Hipparchus compiled the first trigonometric tables around 190 BCE—laying groundwork for functions tied to the unit circle.

The sine function itself, derived from chord lengths in circles, evolved into modern sine through Indian and Islamic scholars, eventually becoming indispensable for navigation and astronomy.

By the Renaissance, trigonometry matured into a computational powerhouse. Mariners used sine and cosine tables to calculate latitude by observing celestial bodies, drastically improving maritime safety and route mapping. The direct influence of these ratios persists: GPS systems depend on precise angle and distance calculations—all rooted in trigonometric identities involving sine, cosine, and tangent.

Even civilization’s physical infrastructure relies on these principles—during construction, engineers apply tangent to determine roof slopes and bridge inclines, ensuring both functionality and safety.

Foundational Roles in Modern Science and Technology

In physics, sine and cosine define wave behavior—from sound oscillations to electromagnetic radiation. The wave equation, vital in Fiber Optics and MRI machines, hinges on these functions to model periodic phenomena. “Sine and cosine are nature’s primary language for rhythmic motion,” notes Dr.

Elena Ramirez, a applied mathematician at MIT. “Their periodicity mirrors the cycles found in light, sound, and quantum states.”

In engineering, tangent emerges as a critical function for slope analysis. Civil engineers compute incline using tan(θ) = rise/run, essential for designing roads, railways, and drainage systems.

“Every span, every grade, depends on tangent to translate force and elevation into buildable reality,” explains structural engineer Marcus Bell. In robotics, forward kinematics—the process of determining end-effector position from joint angles—relies on chaining sine and cosine operations through Denavit-Hartenberg parameters.

Signal processing and telecommunications further depend on these ratios. Fourier transforms, which decompose complex signals into sine and cosine components, underpin everything from audio compression to MRI imaging.

In 5G networks, phase and frequency modulation—governed by trigonometric identities—enable high-speed data transmission. “Without cosine and sine, modern connectivity would collapse,” states networking expert Dr. Rajiv Patel.

“These functions encode the rhythm of real-time data flow across the globe.”

The Triad in Action: Real-World Applications

Consider GPS technology: a satellite transmits a signal, and a receiver calculates its location by measuring the time delay and geometrical angles to multiple satellites. Trigonometry, especially the cosine law in spherical triangles, defines换员工换语 — translation error (pdf, truncated due to interactive environment limits; full article continues fully below in proper HTML css and paragraph flow.) Sine and cosine resolve relative positions across vast distances, while tangent helps decode elevation angles critical for vertical positioning. This synergy enables sub-meter accuracy—transforming navigation from guesswork to precision.

In computer graphics and game development, 3D rendering relies on rotating objects using rotation matrices built on sine and cosine functions. A cube spinning in virtual space shifts via transformations encoded in these ratios, creating lifelike motion that captivates millions of users daily. Even in medical imaging, FSEM (Fourier Shell Correlation) methods use trigonometric transforms to stitch high-resolution images for cancer diagnostics, demonstrating how foundational math drives breakthrough healthcare innovations.

Education and Cognitive Development

Beyond applications, mastering sine, cosine, and tangent cultivates logical