Unlocking Instant Change: How Lnx Derivative Transforms Dynamic Systems Analysis
Unlocking Instant Change: How Lnx Derivative Transforms Dynamic Systems Analysis
In a world where systems evolve in real time—from financial markets to quantum processes—understanding the precise rate of change is critical. The Lnx Derivative emerges as a powerful mathematical tool that captures instantaneous behavioral shifts with unprecedented precision, enabling engineers, scientists, and data analysts to decode complexity at the speed of insight. Unlike traditional derivatives, Lnx Derivative leverages logarithmic differentiation and nonlinear scaling to model rapid transitions, making it indispensable for forecasting, optimization, and control systems across industries.
At its core, Lnx Derivative relies on the logarithmic form of differentiation, where the derivative of a function \( f(x) \) is expressed as \( \frac{d}{dx} \ln f(x) = \frac{f'(x)}{f(x)} \). This transformation compresses growth patterns and reveals multiplicative dynamics often obscured by standard calculus. For systems with exponential or power-law behavior—common in biological networks, chaotic systems, and financial time series—this logarithmic framework unlocks hidden patterns, translating rapid fluctuations into actionable gradients.
Core Principles of Lnx Derivative in System Modeling
The strength of Lnx Derivative lies in its mathematical elegance and practical adaptability.Its formulation enables accurate tracking of instantaneous rates even when underlying processes deviate from smoothness. Key advantages include:
- Enhanced Sensitivity: By measuring relative change rather than absolute differences, Lnx Derivative detects subtle shifts in dynamic systems. This sensitivity proves vital in early anomaly detection, for example, spotting micro-fluctuations in sensor data before they escalate into failures.
- Multiplicative Scaling: Unlike additive noise, logarithmic differentiation amplifies proportional variations, allowing analysts to distinguish meaningful trends from random noise.
This property supports cleaner signal extraction in noisy environments such as satellite telemetry or high-frequency trading streams.
- Nonlinear Response Handling: Systems exhibiting exponential growth, saturation, or feedback loops are modeled more accurately via Lnx Derivative, which captures the true curvature of change. This ensures predictive models reflect real-world complexities without over-simplification.
Applications Across Scientific and Industrial Frontiers
Across domains, Lnx Derivative is proving transformative by enabling high-fidelity modeling of intricate dynamics. In computational biology, researchers use it to map the changing population of enzymes in metabolic pathways, revealing how minute concentration shifts trigger cascading effects.By analyzing logarithmic derivatives of reaction rates, scientists gain early insight into metabolic dysregulation—critical for drug development and personalized medicine. In climate science, Lnx Derivative parses atmospheric data, where rapid changes in greenhouse gas concentrations or oceanic temperature gradients drive unpredictable feedback loops. Its ability to isolate accelerating trends improves the accuracy of climate projections, guiding policy decisions with sharper foresight.
Financial markets benefit equally.
Here, volatility isn’t noise—it’s signal. The Lnx Derivative quantifies instantaneous volatility in asset prices, helping traders execute rapid, data-driven strategies. For algorithmic systems, these real-time derivatives translate microsecond movements into profitable entries and exits, turning ephemeral fluctuations into structured actions.
Engineering applications are profound.
In robotics and control theory, Lnx Derivative refines feedback loops, enabling precise trajectory control in autonomous vehicles and drones. Power systems analysts employ it to monitor grid stability, detecting early signs of imbalance before blackouts occur. Such use cases underscore how Lnx Derivative transforms reactive management into proactive optimization.
Comparative Advantages Over Traditional Derivative Methods
While standard calculus derivatives remain foundational, they often falter when applied to systems characterized by exponential growth, multiplicative noise, or time-varying behavior.Lnx Derivative addresses these limitations by redefining change through logarithmic normalization. This shift allows analysts to:
Bridge discrete data with continuous dynamics more naturally, improving interpolation in sparse datasets.
Model fractal-like patterns common in natural systems—from turbulence to neural spikes—with greater fidelity than polynomial or piecewise approximations.
Enhance machine learning pipelines by integrating log-derivative features that boost model robustness during training on volatile or non-stationary data.
“Traditional derivatives treat change linearly, missing the exponential undercurrents that drive real-world systems,” explains Dr. Elena Marquez, a computational physicist at the Max Planck Institute.“Lnx Derivative isn’t just a mathematical tool—it’s a lens. It reveals the hidden currents behind rapid transitions, making prediction not just possible, but precise.”
Practical Considerations and Implementation Challenges
Despite its power, deploying Lnx Derivative demands careful attention to data quality and context. The logarithmic transformation is undefined for zero or negative values, requiring preprocessing and interval constraints—particularly critical in economic or environmental datasets with intermittent zero states.Moreover, while robust, improper normalization can amplify measurement errors; outlier filtering and data smoothing remain essential preprocessing steps. Integrating Lnx Derivative into existing analytical workflows often involves custom coding, though several open-source libraries and Python-based toolkits—such as MathInfo and LogDerivPy—simplify implementation. These tools automate logarithmic scaling, error handling, and numerical stability, lowering entry barriers for practitioners across scientific and industrial sectors.
Future Trajectory: From Research Tool to Industry Standard
As systems grow more complex and data volumes explode, Lnx Derivative is poised to transition from niche research tool to cornerstone of dynamic analytics.Its capacity to distill rapid change into actionable gradients positions it at the forefront of advancements in predictive modeling, autonomous systems, and real-time decision engines. Emerging applications in quantum computing—where qubit states evolve at light speed—and personalized genomics—driven by real-time biomarker tracking—demand precisely this level of sensitivity. Early adopters are already pioneering frameworks where Lnx Derivative powers adaptive control, predictive diagnostics, and self-optimizing networks.
In finance, energy, and healthcare, its influence will deepen, transforming how institutions anticipate, respond to, and shape change. Beyond incremental improvement, Lnx Derivative represents a paradigm shift. It enables scientists and engineers not just to measure change—but to understand it, predict it, and harness it.
In an era of accelerating complexity, the ability to compute instantaneous transformation is no longer optional. It is the next frontier of insight.
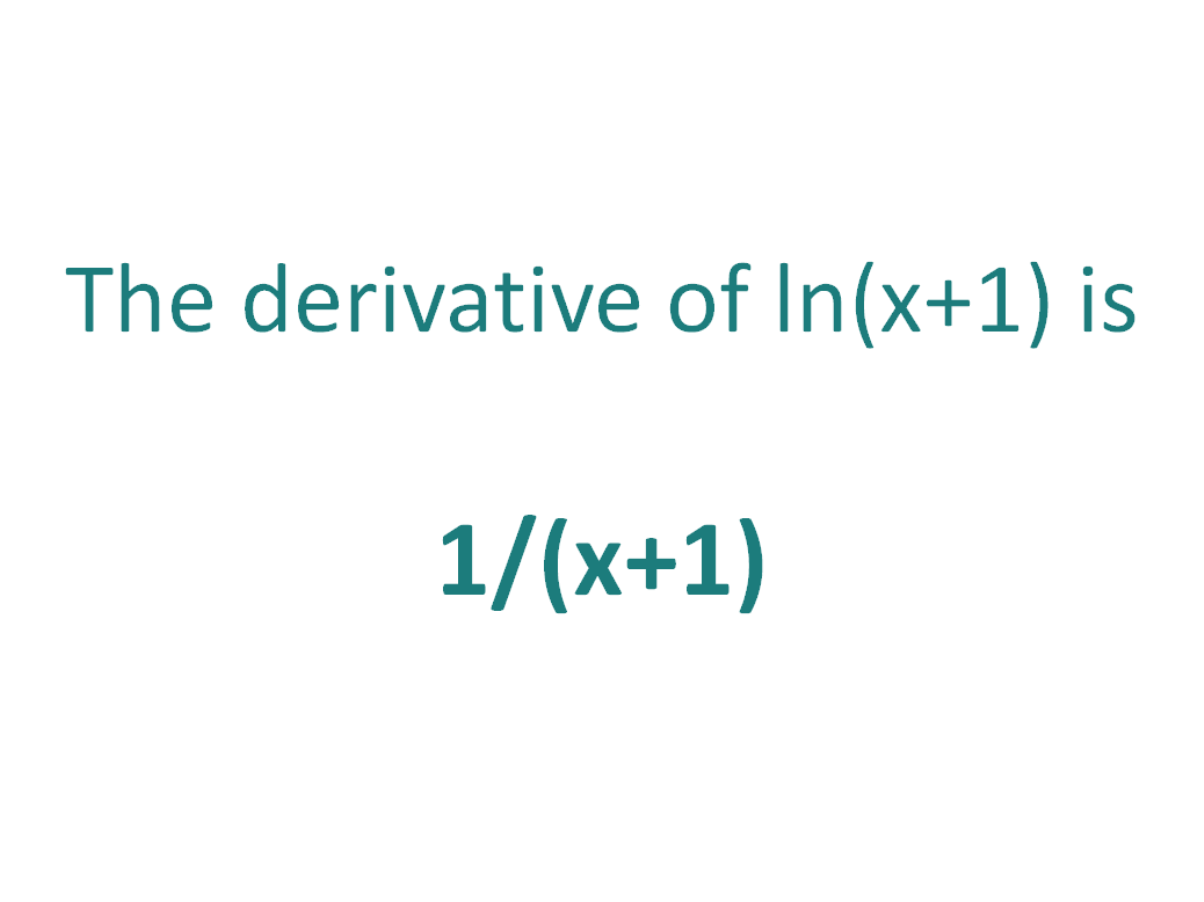
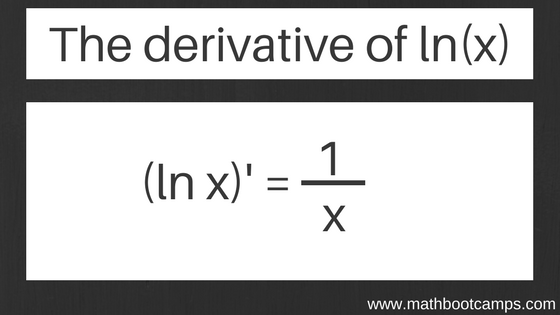
![What is the Derivative of lnx^2 [Solved] - iMath](https://www.imathist.com/wp-content/uploads/2024/02/Derivative-of-lnx^2.webp)
Related Post

For Better or For Worse: The Enduring Legacy of the Iconic Comic Strip

Unveiling The Wealth Of A Rising Star: The Growing Net Worth Of Chico Lachowski

Master Persona 3 Fusion Calculator Like a Pro: Unlock Perfect Combat & Character Synergy

Young And The Restless’ Victor Leaving Sparks Waves Across Soapy Drama Field

